fun calculations

I'm not sure what I did on weekdays at 9pm during my earliest years but after 2000 the answer was simple. I was watching The Simpsons on The Comedy Network. Most of my middle school friends were doing the same and this put us in a position to witness the end of an era. Reruns that aired every day seemed strikingly different from the new episodes that aired on Sunday and it did not take us long to figure out that the latter were steadily getting worse. The decline of The Simpsons is common knowledge but I recently found a visualization which puts it in a rather harsh perspective. This chart, by filmmaker Sol Harris, points out among other things that The Simpsons has more than twice as many episodes as the next longest running cartoon. The writers would be able to take 14 years off to come up with good ideas again and still be able to call themselves the record holders. I would say the tail is so long that some viewers, who have already been watching for a number of years, were born after the last good episode.

But what is the last good episode? Modulo some broken clocks that are right twice a day, Harris tells us that it is the 12th Halloween special which aired at the beginning of season 13. The episode afterwards called "The Parent Rap" is scorned as "the definitive moment when the show went from 'Bad Simpsons' to 'Bad Television'". In the Harris ratings, which I have re-plotted above, the beginning of season 13 indeed looks like a turning point. A more satisfying exercise is to justify this with maximum likelihood estimation.

There is a party game called Zombie Dice where you roll dice and try to get as many points as you can without losing all of your health and dying. Green dice make points more likely than death, red dice make death more likely than points and yellow dice are neutral. I played it with some friends awhile ago and realized that it was probably simple enough for me to come up with the optimal strategy.

Just about every game is solvable in principle, but it is very easy to make a game that would take longer than the age of the universe to solve. The prototypical solved game is tic-tac-toe. The prototypical game that is still a long way from being solved is chess. An xkcd comic lists a bunch of solved games so let's see how we can add Zombie Dice to this list.

It's the holiday season. And that means I get to be reminded of how logical air travel is. One of the most annoying things is that I can't take everything as carry-on luggage. Don't get me wrong, I hardly bring anything. But two things I usually bring are a razor and shaving cream which security guards tend to take away. Because of that, the idea of checking in online saves no time at all. Here's what the screen should really say:

Nevertheless, I got to the airport on time and was able to stay relatively occupied on the plane.

Lines drawn on a curved surface can be tricky. Consider one of the most basic facts about Euclidean geometry: that parallel lines never intersect. This does not hold on the surface of the Earth. If you and a friend stand one metre apart in some location on the Earth, you could both try drawing a line and heading due north. The lines would appear to be parallel during all stages of the journey but you would eventually find that they intersect at the North Pole. An observer watching from space would say that the lines don't look parallel but any measurement you could make without leaving the Earth would tell you that they are. This is because a sphere is locally flat. The fact that the lines cross can therefore be used to prove that the world is round. Similarly, measurements done in three dimensional space, might be able to prove things like that about the universe.

Now it's not just parallel lines that we have to worry about. If space were not flat, circle areas would appear to differ from and the sum of the angles in a triangle would appear to differ from . There is a wonderful formalism for doing calculus with lines drawn on a curved surface and there are two contexts in which people normally learn it. One is navigation and the other is general relativity. I want to take a shot at explaining it in the context of the two ant problem. This requires us to find the shortest distance between two points on a curved surface and prove it is the shortest. So if I hadn't already solved the problem, it might seem appropriate to use the techniques that were historically used to prove that a straight line is the shortest path between two points in flat space and that a great circle is the shortest path between two points on a sphere.

Two and a half years ago, I worked for a teaching program at Queen's that could help first year calculus students get extra marks. It was called Math Investigations and its purpose was to show interesting problems that students might not see in a regular class. As a third year math student, I could solve most of them in a brief sitting but one problem called "two ants" eluded us and it just happened to be the first problem we presented.

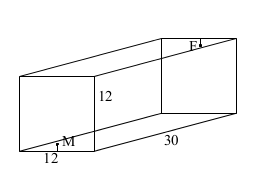
My partner for TA'ing that section was James McLean and we were later joined by Rob Wang. We downloaded problem sets picked out by the head of the program - Peter Taylor - and he also happens to list the ant problem first. The premise is that a 12x12x30 box houses a male ant and a female ant and they are located on the square ends. One is eleven twelfths of the way between the floor and the ceiling, the other is eleven twelfths of the way between the ceiling and the floor. One ant wants to meet the other by crawling on the surface of the box - taking the shortest possible path. If you read the solution we were given, you will see that it does not prove which path is the shortest or give a real indication of how one might do so.

What's a fun thing to do when you learn a less than intuitive concept? Searching the web to find another person's opinion of it! I recently learned about Grassman numbers and my search turned up a blog post by a professor named Luboš Motl who makes some pretty debatable claims. After reading the post, I found out that he is actually quite famous. So yes, he probably knows much more than me about the subject, but I must still object to how complacent he is with using an object and not defining it.

There are plenty of cases where a proof written down by a physicist is worse than a proof written down by a mathematician, but this is a particularly bad one. In one of my courses, we got to derive the Dirac matrices, which are instrumental in describing spin 1/2 particles. These four matrices are written as with an index. One definition of them says that they should satisfy the anti-commutation relations of the Clifford algebra:

where is the Minkowski metric from special relativity.

How big do our matrices have to be in order to satisfy this? They obviously cannot be 1x1 matrices because these are just numbers that commute. It turns out that they have to be at least 4x4 but all published sources I have seen fail at explaining why. I will go through the physics proof that is often given and then set the record straight by writing a real proof. If it appears nowhere else, let it appear here!

As part of a summer internship, I got to put together several electronic components, and for the first time, use something more permanent than a breadboard. I found my first circuit very frustrating because my solder connections kept coming loose and I was told to make it as small as possible. But seriously... am I so used to learning about algebraic varieties and Feynman diagrams that I have become allergic to learning a real transferable skill?

The need for my first circuit arose because the photodiode that we used to measure the power in various lasers had a proportionality constant that was too small. For every Watt of power, the diode was calibrated to put only across two pins. We wanted to amplify this to a larger value. The component typically used for these applications that you can buy off the shelf is the operational amplifier.

In a recent post, we used trigonometry to derive the length of a day on the Earth as a function of the observer's latitude and the time of year. As promised, I want to continue modelling the Earth's orbit to see what it can tell us about temperature. The simplest explanation for the seasonal variation of temperature comes from the concept of solar flux. To see what this means, think about taking a ray of sunlight shining on the Earth and decomposing it into two components - one parallel to the Earth's surface and one perpendicular.

Most of the sunlight going into the ground means this location will be hot, whereas most of the sunlight going along the ground means this location will be cold. The temperature due to direct sunlight is therefore proportional to the cosine of the angle between the ray and the outward normal to the Earth. To actually solve for a temperature, we would have to multiply the intensity of the light by and integrate this over a region of interest. Our main concern will be solving for , allowing us to express the temperature at one time relative to the temperature at another time without knowing the absolute intensity.

Two and a half years ago, when I read the research interests of my statistics prof, I noticed that he had become interested in analyzing epidemiological models. Now, I might finally understand what he was talking about.

If we let S be the population of individuals who are susceptible to the disease, I be the population infected with it and R the population that has recovered, it is not too big a stretch to say that this plot appears to follow the progression of a non-lethal disease. Only a small number of people have the disease at the beginning, but this number grows because the disease is contagious. People who have recovered are immune to further infection meaning that the epidemic eventually dies out.