Main menu
You are here
Those Physicists And Their "Physics Proofs"
There are plenty of cases where a proof written down by a physicist is worse than a proof written down by a mathematician, but this is a particularly bad one. In one of my courses, we got to derive the Dirac matrices, which are instrumental in describing spin 1/2 particles. These four matrices are written as 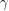 with an index. One definition of them says that they should satisfy the anti-commutation relations of the Clifford algebra:
with an index. One definition of them says that they should satisfy the anti-commutation relations of the Clifford algebra:
![\[<br />
\left \{ \gamma^{\mu}, \gamma^{\nu} \right \} \equiv \gamma^{\mu}\gamma^{\nu} + \gamma^{\nu}\gamma^{\mu} = 2 \eta^{\mu\nu} I<br />
\]](/sites/default/files/tex/07715676691314b849ab17ed1c665550d3ff6954.png) |
where 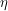 is the Minkowski metric from special relativity.
is the Minkowski metric from special relativity.
![\[<br />
\eta = \left [<br />
\begin{tabular}{cccc}<br />
1 & 0 & 0 & 0 \\<br />
0 & -1 & 0 & 0 \\<br />
0 & 0 & -1 & 0 \\<br />
0 & 0 & 0 & -1<br />
\end{tabular}<br />
\right ]<br />
\]](/sites/default/files/tex/cc398a09e9aaf8f99f4b401fcc945cfc09674962.png) |
How big do our matrices have to be in order to satisfy this? They obviously cannot be 1x1 matrices because these are just numbers that commute. It turns out that they have to be at least 4x4 but all published sources I have seen fail at explaining why. I will go through the physics proof that is often given and then set the record straight by writing a real proof. If it appears nowhere else, let it appear here!
Incomplete proof
I will depart from the convention of calling the matrices 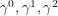 and
and 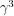 . For some reason I like
. For some reason I like 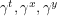 and
and 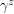 better. The relations above basically say that:
better. The relations above basically say that:
![\[<br />
\left ( \gamma^t \right )^2 = I, \;\;\; \left ( \gamma^i \right )^2 = -I<br />
\]](/sites/default/files/tex/2f84edabdbd4936d35b6647f90d9ea9bfae72ae2.png) |
and distinct Dirac matrices anti-commute. If we look at the equation 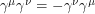 and take the determinant of both sides, we get:
and take the determinant of both sides, we get: 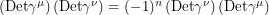 . If something is equal to
. If something is equal to 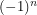 times itself,
times itself,  must be even. This rules out 3x3 Dirac matrices and the question becomes why can't we represent the Clifford algebra with 2x2 matrices?. Most physics textbooks seem to be okay with this part of the proof.
must be even. This rules out 3x3 Dirac matrices and the question becomes why can't we represent the Clifford algebra with 2x2 matrices?. Most physics textbooks seem to be okay with this part of the proof.
Some people say that the largest possible set of anti-commuting 2x2 matrices has only three elements. Is this supposed to be easy to show? Is the maximal anti-commuting set known for matrices of any size? There is a paper about that from 1932. It is 11 pages and only proves the 4x4 case so I highly doubt it. Anyway, here is how other sources proceed to "prove" this result:
We know that the three Pauli matrices anti-commute so let three of our Dirac matrices be Pauli matrices. Also, if we take the three Pauli matrices and adjoin the identity, we get a basis for the vector space of 2x2 matrices. Therefore our fourth Dirac matrix must be expressed as:
![\[<br />
M = a_t I + a_x \sigma_x + a_y \sigma_y + a_z \sigma_z<br />
\]](/sites/default/files/tex/bdc5a97c21dd21e56d0086e64ad01097279f1a76.png) |
Since the Pauli matrices anti-commute, the product of distinct Pauli matrices will be traceless (as is a single Pauli matrix). The trace of a squared Pauli matrix is 2. Therefore by linearity, 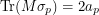 . However,
. However, 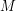 also has to anti-commute with
also has to anti-commute with 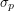 meaning that
meaning that 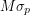 should be traceless. This forces
should be traceless. This forces 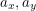 and
and 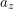 to all be zero meaning
to all be zero meaning 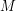 is the identity. The identity commutes with every matrix so the fourth matrix we set out to find doesn't exist.
is the identity. The identity commutes with every matrix so the fourth matrix we set out to find doesn't exist.
This works if you restrict yourself to a ridiculously special case but who ever said that three of the four anti-commuting matrices should be Pauli matrices? Maybe if you start off with a different set of three anti-commuting matrices there suddenly will be room for a fourth. The proof above would only be complete if it cited some theorem that this never happens. Since I am not aware of such a theorem, I will split our search into two cases and show that in each case we can only find three matrices with the desired properties, not four.
Complete proof
Notice that the equations defining our Dirac matrices are invariant under similarity transformations. If 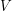 is an invertible matrix,
is an invertible matrix,
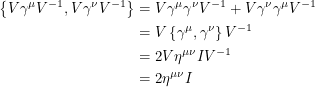 |
so without loss of generality, we can assume that 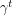 is in Jordan canonical form. Case 1: assume that
is in Jordan canonical form. Case 1: assume that 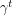 is diagonalizable. You get the identity by squaring
is diagonalizable. You get the identity by squaring 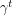 so the diagonal entries in it can only be
so the diagonal entries in it can only be 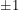 . If both diagonal entries had the same sign, we would be left with a matrix that commutes with everything. Therefore in this case,
. If both diagonal entries had the same sign, we would be left with a matrix that commutes with everything. Therefore in this case, 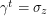 . Denote the components of
. Denote the components of 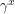 by
by 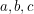 and
and 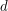 . The fact that
. The fact that 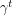 anti-commutes with
anti-commutes with 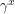 says that:
says that:
![\begin{align*}<br />
\left [<br />
\begin{tabular}{cc}<br />
1 & 0 \\<br />
0 & -1<br />
\end{tabular}<br />
\right ] \left [<br />
\begin{tabular}{cc}<br />
a & b \\<br />
c & d<br />
\end{tabular}<br />
\right ] &= - \left [<br />
\begin{tabular}{cc}<br />
a & b \\<br />
c & d<br />
\end{tabular}<br />
\right ] \left [<br />
\begin{tabular}{cc}<br />
1 & 0 \\<br />
0 & -1<br />
\end{tabular}<br />
\right ] \\<br />
\left [<br />
\begin{tabular}{cc}<br />
a & b \\<br />
-c & -d<br />
\end{tabular}<br />
\right ] &= \left [<br />
\begin{tabular}{cc}<br />
a & -b \\<br />
c & -d<br />
\end{tabular}<br />
\right ]<br />
\end{align*}](/sites/default/files/tex/2de02e02e9c468f879b44680397f0ca7fcf69e33.png) |
In other words, 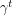 being diagonal forces the spatial Dirac matrices to be anti-diagonal. Now we will let
being diagonal forces the spatial Dirac matrices to be anti-diagonal. Now we will let 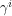 have the entry
have the entry 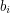 in the upper right and
in the upper right and 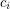 in the lower left. If these matrices all anti-commute, the equations that this gives us are:
in the lower left. If these matrices all anti-commute, the equations that this gives us are:
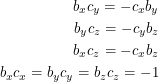 |
where the last equation comes from squaring the spatial Dirac matrices. Multiply the first equation by 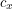 . This gives
. This gives 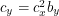 . If we substitute this into the second equation we get
. If we substitute this into the second equation we get 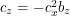 . Now substituting this into the third equation,
. Now substituting this into the third equation, 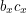 comes out to
comes out to 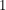 , contradicting the last equation. Therefore starting with a diagonal
, contradicting the last equation. Therefore starting with a diagonal 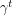 leads to a contradiction.
leads to a contradiction.
Case 2: if 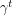 is not diagonalizable, its Jordan form is:
is not diagonalizable, its Jordan form is:
![\[<br />
\left [<br />
\begin{tabular}{cc}<br />
\lambda & 1 \\<br />
0 & \lambda<br />
\end{tabular}<br />
\right ]<br />
\]](/sites/default/files/tex/5d6f2d53f0b85444dba7a2ee209ac557f1585292.png) |
However, the square of this matrix has 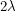 in an off-diagonal entry. We know
in an off-diagonal entry. We know 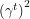 is diagonal so it is necessary to have
is diagonal so it is necessary to have 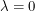 but this is not sufficient to give us
but this is not sufficient to give us 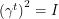 . The square of the above matrix with
. The square of the above matrix with 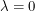 will be the zero matrix, not the identity. Therefore this 2x2 Dirac matrix assumption is a contradiction too and we must use matrices that are 4x4 or larger.
will be the zero matrix, not the identity. Therefore this 2x2 Dirac matrix assumption is a contradiction too and we must use matrices that are 4x4 or larger.
This completes the proof without automatically assuming that everything is a Pauli matrix. It is worth noting however that the Dirac matrices can be expressed quite nicely in terms of the Pauli matrices. It is easy to check that the following expressions satisfy the Clifford algebra relations:
![\[<br />
\gamma^t = \left [<br />
\begin{tabular}{cc}<br />
0 & I \\<br />
I & 0<br />
\end{tabular}<br />
\right ], \;\;\; \gamma^i = \left [<br />
\begin{tabular}{cc}<br />
0 & \sigma_i \\<br />
\sigma_i & 0<br />
\end{tabular}<br />
\right ]<br />
\]](/sites/default/files/tex/f44c4583e7812af1e06ca3ae5747bfd258caa803.png) |
This close resemblance explains why I want to treat the Dirac and Pauli matrices symmetrically. I learned about the Pauli matrices first which were subscripted using x, y, z instead of 1, 2, 3. This is why I reject the idea of using numbers instead of letters on the Dirac matrices. I also refuse to call them "gamma matrices" because no one ever used "sigma matrix" to refer to a Pauli matrix. No I will not dare to compare myself to Dirac even though he used his own "symmetry conventions" to decide on terminology. Oh wait, I just did.
