Main menu
You are here
So I Felt Like Solving Zombie Dice
| There is a party game called Zombie Dice where you roll dice and try to get as many points as you can without losing all of your health and dying. Green dice make points more likely than death, red dice make death more likely than points and yellow dice are neutral. I played it with some friends awhile ago and realized that it was probably simple enough for me to come up with the optimal strategy. |

|
Just about every game is solvable in principle, but it is very easy to make a game that would take longer than the age of the universe to solve. The prototypical solved game is tic-tac-toe. The prototypical game that is still a long way from being solved is chess. An xkcd comic lists a bunch of solved games so let's see how we can add Zombie Dice to this list.
Now the rules of Zombie Dice are that you have a cup containing 13 dice and on your turn, you randomly choose dice to roll. You always roll three at a time and you can keep doing this until you die, run out of dice or choose to pass the cup on to the next person. There are three icons that can be rolled:
- Brains: Each brain is a point. The possibility of more brains would encourage a person to keep rolling. Green dice have three, yellow have two and red have one.
- Shotguns: Shotgun blasts lower your health by one, and if three of them are encountered in a turn, the turn ends with 0 points. The possibility of more shotguns would discourage one from continuing to roll. Green dice have one, yellow have two and red have three.
- Walkers: Denoted by footprints, this result means that the die will be included in the next roll if you choose to roll again. Instead of drawing three new dice, you draw three minus the number of walkers from the last roll. All dice have two of these.
The cup begins with 6 green dice, 4 yellow dice and 3 red dice. The first player to get 13 points wins. This can be done in one turn but the probability is about one in a million. The need for some basic strategy is clear. You could end up with three green dice for your first roll and then roll them and get a lot of brains, which is good. But this makes the second roll more risky. The fact that three green dice have been used up means that the next dice are more likely to be yellow and red which increase your chances of being shot. This uncertainty about whether to roll is part of the fun of the game. It can be surmounted by using a formula for the expected number of points 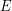 . When deciding whether to continue, a player should roll if
. When deciding whether to continue, a player should roll if 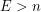 and cash in if
and cash in if 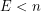 .
.
The game state is a function of a few different variables. First, you need to know how many green dice are left 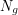 , how many yellow dice are left
, how many yellow dice are left 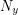 and how many red dice are left
and how many red dice are left 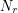 . You also need to know your health
. You also need to know your health 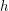 and the number of points you already have
and the number of points you already have  . Also dictating the state of the game are the number of walkers you have and the colours of the dice on which they appear. The initial condition is
. Also dictating the state of the game are the number of walkers you have and the colours of the dice on which they appear. The initial condition is 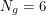 ,
, 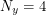 ,
, 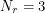 ,
, 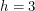 and
and 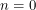 with no walkers.
with no walkers.
If a player rolls three walkers, the following roll would just be a re-roll so in this case
![\[<br />
E = E_{w_1, w_2, w_3} (n, h)<br />
\]](/sites/default/files/tex/46ec5a2c84398ec32020b76ba6769de04bc23e5a.png) |
Rolling two walkers on the other hand, requires the player to draw one die. This can either be a green, a yellow or a red die so there are three expectation values to consider. Moreover they must be weighted by the probability that the given die will be drawn so the overall expected number of points is
![\begin{align*}<br />
E &= P(g|N_g, N_y, N_r) E_{w_1, w_2, g} (n, h) + P(y|N_g, N_y, N_r) E_{w_1, w_2, y} (n, h) + P(r|N_g, N_y, N_r) E_{w_1, w_2, r} (n, h) \\<br />
&= \frac{1}{N_g + N_y + N_r} \,\, \left [ N_g E_{w_1, w_2, g} (n, h) + N_y E_{w_1, w_2, y} (n, h) + N_r E_{w_1, w_2, r} (n, h) \right ]<br />
\end{align*}](/sites/default/files/tex/edba9f5778c3a381b5d438be3995b526963fd5e1.png) |
where in the last step I have written in the expressions for how likely it is that a given die will be drawn. With one walker, there are two dice to be drawn leading to a weighted sum of six conditional expectations:
![\begin{align*}<br />
E &= P(g, g|N_g, N_y, N_r) E_{w, g, g} (n, h) + P(y, y|N_g, N_y, N_r) E_{w, y, y} (n, h) + P(r, r|N_g, N_y, N_r) E_{w, r, r} (n, h) \\<br />
&+ P(g, y|N_g, N_y, N_r) E_{w, g, y} (n, h) + P(g, r|N_g, N_y, N_r) E_{w, g, r} (n, h) + P(y, r|N_g, N_y, N_r) E_{w, y, r} (n, h) \\<br />
&= \frac{1}{\binom{N_g + N_y + N_r}{2}} \, \left [ \binom{N_g}{2} E_{w, g, g} (n, h) + \binom{N_y}{2} E_{w, y, y} (n, h) + \binom{N_r}{2} E_{w, r, r} (n, h) \right \none \\<br />
&\left \none + N_g N_y E_{w, g, y} (n, h) + N_g N_r E_{w, g, r} (n, h) + N_y N_r E_{w, y, r} (n, h) \right ]<br />
\end{align*}](/sites/default/files/tex/3527f03b93463e79d8c157cdafddc36e3d97fc2f.png) |
With no walkers and no dice pre-determined, we get ten terms in the sum:
![\begin{align*}<br />
E &= P(g, g, g|N_g, N_y, N_r) E_{g, g, g} (n, h) + P(g, g, y|N_g, N_y, N_r) E_{g, g, y} (n, h) + P(g, g, r|N_g, N_y, N_r) E_{g, g, r} (n, h) \\<br />
&+ P(y, y, y|N_g, N_y, N_r) E_{y, y, y} (n, h) + P(y, y, g|N_g, N_y, N_r) E_{y, y, g} (n, h) + P(y, y, r|N_g, N_y, N_r) E_{y, y, r} (n, h) \\<br />
&+ P(r, r, r|N_g, N_y, N_r) E_{r, r, r} (n, h) + P(r, r, g|N_g, N_y, N_r) E_{r, r, g} (n, h) + P(r, r, y|N_g, N_y, N_r) E_{r, r, y} (n, h) \\<br />
&+ P(g, y, r|N_g, N_y, N_r) E_{g, y, r} (n, h) \\<br />
&= \frac{1}{\binom{N_g + N_y + N_r}{3}} \left [ \binom{N_g}{3} E_{g, g, g} (n, h) + N_y \binom{N_g}{2} E_{g, g, y} (n, h) + N_r \binom{N_g}{2} E_{g, g, r} (n, h) \right \none \\<br />
&\left \none + \binom{N_y}{3} E_{y, y, y} (n, h) + N_g \binom{N_y}{2} E_{y, y, g} (n, h) + N_r \binom{N_y}{2} E_{y, y, r} (n, h) \right \none \\<br />
&\left \none + \binom{N_r}{3} E_{r, r, r} (n, h) + N_g \binom{N_r}{2} E_{r, r, g} (n, h) + N_y \binom{N_r}{2} E_{r, r, y} (n, h) \right \none \\<br />
&\left \none + N_g N_y N_r E_{g, y, r} (n, h) \right ]<br />
\end{align*}](/sites/default/files/tex/45f2a52bb9376bcc8834184b9f822c7520dec024.png) |
Once we know the ten expected values, these four expressions allow us to plug in the game state and always know whether it makes sense to keep betting or fold. The expectations are tedious to calculate but I didn't come this far to back down now! Here is a list of them:
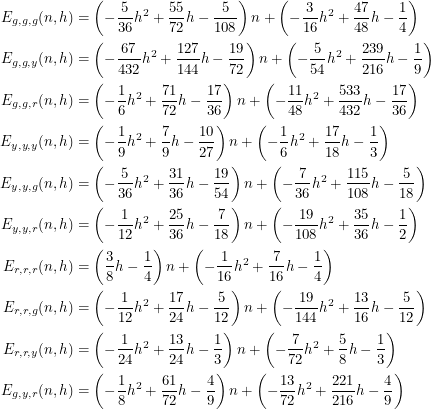 |

As an example I will repeat one of the calculations here. How about
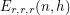 , the one with three red dice. Whenever you begin a roll with
, the one with three red dice. Whenever you begin a roll with  points, there are five possibilities for the number of points you will have at the end of the roll:
points, there are five possibilities for the number of points you will have at the end of the roll: 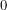 ,
,  ,
, 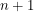 ,
, 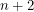 or
or 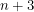 . One definite thing we can say is that
. One definite thing we can say is that 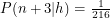 because in order to get three points, we need to roll three brains in a row. Every other probability depends on what the health is. First, let's solve for them when the player has three health.
because in order to get three points, we need to roll three brains in a row. Every other probability depends on what the health is. First, let's solve for them when the player has three health.
![\[<br />
P(0|h=3) = \left ( \frac{1}{2} \right )^3 = \frac{1}{8}<br />
\]](/sites/default/files/tex/923b92ac9489d91c08d2bcb7f5869ee9c55ea0e3.png) |
because in order to die and lose all your points, you would have to roll three shotgun blasts in a row. In order to gain or lose no points, you have to roll three non-brains without dying.
![\[<br />
P(n|h=3) = \left ( \frac{5}{6} \right )^3 - \frac{1}{8} = \frac{49}{108}<br />
\]](/sites/default/files/tex/6806767067551a9dae43539e551605e75a4d2218.png) |
The first product is the probability for rolling three non-brains in a row. This counts the possibility of three shotguns however which is why we subtract one eighth.
![\[<br />
P(n+1|h=3) = 3 \left ( \frac{1}{6} \right ) \left ( \frac{5}{6} \right )^2 = \frac{25}{72}<br />
\]](/sites/default/files/tex/58fd6c2c5340cc2a7c639bad455c509a8b69f059.png) |
If we want one additional point, we are rolling one brain and two non-brains. We multiply by three because any one of the three red dice could've been the one that was a brain.
![\[<br />
P(n+2|h=3) = 3 \left ( \frac{1}{6} \right )^2 \left ( \frac{5}{6} \right ) = \frac{5}{72}<br />
\]](/sites/default/files/tex/8c595b2cfe8117fcd26921c9dce873aefef0f3e4.png) |
For two additional points, we do the same thing except it's two brains and one non-brain. Plugging these into the formula for expected value,
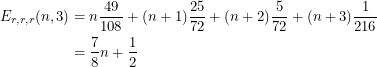 |
Moving on to two health,
![\[<br />
P(0|h=2) = \left ( \frac{1}{2} \right )^2 + 3 \left ( \frac{1}{2} \right )^3 = \frac{1}{2}<br />
\]](/sites/default/files/tex/ba63c9a1f9eafea16a0a68d7b465e91644d36083.png) |
we get an extra term in the probability of dying compared to three health. We could roll the three shotgun outcome from our last calculation but we also need to count the three ways of rolling two shotguns and one non-shotgun.
![\[<br />
P(n|h=2) = \left ( \frac{1}{3} \right )^3 + 3 \left ( \frac{1}{3} \right )^2 \left ( \frac{1}{2} \right ) = \frac{11}{54}<br />
\]](/sites/default/files/tex/80dd640e943a48906d88f2059ca67cd295e9fb00.png) |
Here, the first term is the probability of three walkers and the second is the probability of two walkers and a shotgun.
![\[<br />
P(n+1|h=2) = 3 \left ( \frac{1}{6} \right ) \left ( \frac{1}{3} \right )^2 + 6 \left ( \frac{1}{2} \right ) \left ( \frac{1}{3} \right ) \left ( \frac{1}{6} \right ) = \frac{2}{9}<br />
\]](/sites/default/files/tex/f284b82d2618807b9755c5d12fd7c6283a5310a0.png) |
This is brain-walker-walker plus brain-walker-shotgun. The six is there because there are six permutations we can apply to the three different values.
![\[<br />
P(n+2|h=2) = 3 \left ( \frac{1}{6} \right )^2 \left ( \frac{1}{3} \right ) + 3 \left ( \frac{1}{6} \right )^2 \left ( \frac{1}{2} \right ) = \frac{5}{72}<br />
\]](/sites/default/files/tex/ca37bb5e5bc992cb21d7010fca6f11f38f223016.png) |
This one is brain-brain-walker plus brain-brain-shotgun. Now we can plug these in again to get
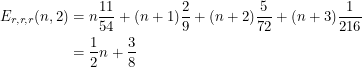 |
Notice that this roll puts you at a disadvantage unless you have zero points and nothing to lose. This is in contrast to the same roll at three health where you need to have four points before the roll becomes too dangerous. Now to deal with the case of one health,
![\[<br />
P(0|h=1) = 1-\left ( \frac{1}{2} \right )^3 = \frac{7}{8}<br />
\]](/sites/default/files/tex/c23b43df982b324ba19c5dfe324fe728c4e54b83.png) |
Everything but three non-shotguns leads to death so we simply subtract this probability from unity.
![\[<br />
P(n|h=1) = \left ( \frac{1}{3} \right )^3 = \frac{1}{27}<br />
\]](/sites/default/files/tex/2d37ccc6ff45b7f4cdbc482088cebeca65cbd58f.png) |
For this one, a single shotgun would kill us and a single brain would give us a point, so it's walker-walker-walker.
![\[<br />
P(n+1|h=1) = 3\left ( \frac{1}{6} \right ) \left ( \frac{1}{3} \right )^2 = \frac{1}{18}<br />
\]](/sites/default/files/tex/30dbfdd3f457702b1edd73954934634369ece9ff.png) |
This has to be brain-walker-walker for the same reason.
![\[<br />
P(n+2|h=1) = 3\left ( \frac{1}{6} \right )^2 \left ( \frac{1}{3} \right ) = \frac{1}{36}<br />
\]](/sites/default/files/tex/4b859e5119e6101e49f8ac2ec1910bb4f7f0fe2c.png) |
Similarly, this is brain-brain-walker. Now to plug in these numbers one more time,
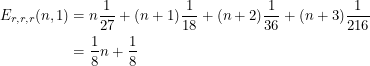 |
Now we have three equations but we want to combine them into one that looks like 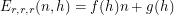 . This is just a cheap trick so we will choose quadratics
. This is just a cheap trick so we will choose quadratics 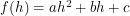 ,
, 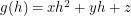 . The requirements
. The requirements 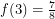 ,
, 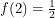 ,
, 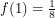 ,
, 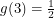 ,
, 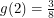 and
and 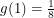 reduce this to a system of linear equations. Solving them, we get
reduce this to a system of linear equations. Solving them, we get 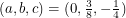 and
and 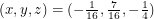 . Of the ten tedious functions of
. Of the ten tedious functions of  and
and 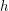 , this gives us the seventh one. The others are all obtained in similar ways.
, this gives us the seventh one. The others are all obtained in similar ways.
Clearly by taking your first roll, you can only gain points or stay the same. Subsequent rolls only happen if you stand to benefit from them. Therefore a turn will give a player more than zero points on average. In other words, the game will almost surely end. A harder calculation would tell you how many turns this is likely to take. This is the same as asking what the expectation is for the number of points that can be accumulated in a single turn if this optimal strategy is used from start to finish. In fact one could get the entire distribution for the number of points accumulated. This is mainly hard because of the walkers. The events of rolling a certain outcome and choosing a certain set of dice for the next roll are not independent. Maybe we should simulate this. Sorry for switching between first, second and third person so often.
