Main menu
You are here
Ants On A Box
Two and a half years ago, I worked for a teaching program at Queen's that could help first year calculus students get extra marks. It was called Math Investigations and its purpose was to show interesting problems that students might not see in a regular class. As a third year math student, I could solve most of them in a brief sitting but one problem called "two ants" eluded us and it just happened to be the first problem we presented.
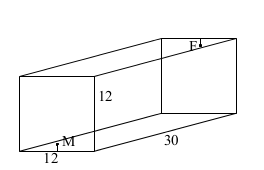
My partner for TA'ing that section was James McLean and we were later joined by Rob Wang. We downloaded problem sets picked out by the head of the program - Peter Taylor - and he also happens to list the ant problem first. The premise is that a 12x12x30 box houses a male ant and a female ant and they are located on the square ends. One is eleven twelfths of the way between the floor and the ceiling, the other is eleven twelfths of the way between the ceiling and the floor. One ant wants to meet the other by crawling on the surface of the box - taking the shortest possible path. If you read the solution we were given, you will see that it does not prove which path is the shortest or give a real indication of how one might do so.
Finding the shortest distance "as the crow flies" is trivial, but it is harder to find the shortest path among those constrained to the box. The approach favoured by the notes is to unfold the box in a few different ways and compare the lengths of a few different paths you can draw when the box is unfolded. You can get different lengths depending on how you unfold it.
|
|
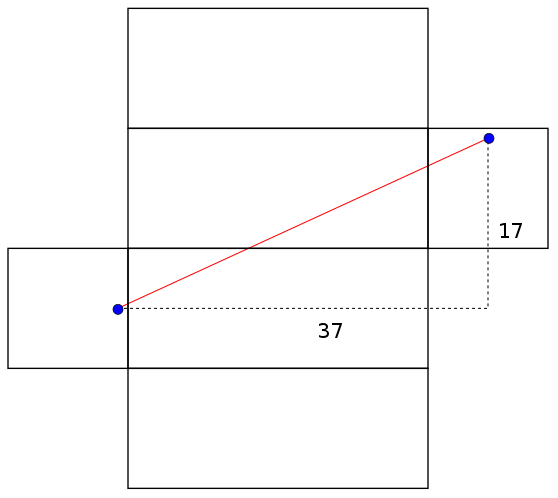
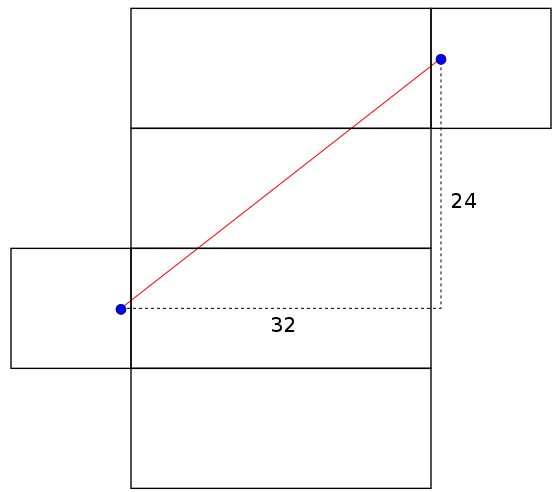
This is what we were supposed to be teaching - that you should keep trying to improve your answer rather than being satisfied so easily. Two admissible nets for the box are shown above and one path length is
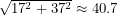 while the other is
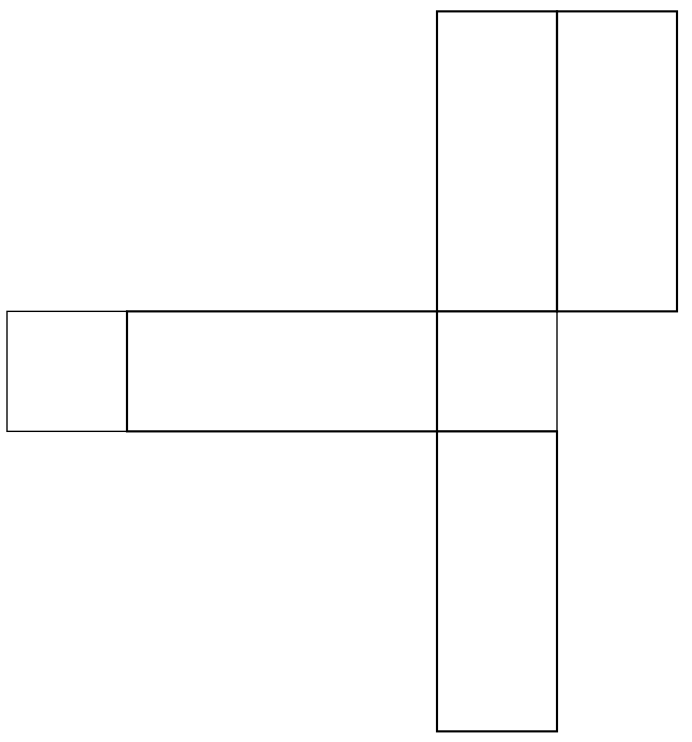
while the other is 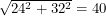 . The notes claim without proof that the path on the right is the shortest path joining the two ants that one can ever find. How many times do we have to unpack the box in order to prove this?
. The notes claim without proof that the path on the right is the shortest path joining the two ants that one can ever find. How many times do we have to unpack the box in order to prove this?
What we are doing is mapping the box onto the plane in a way that preserves distance. A function between different surfaces that preserves distance is called an isometry. Since we know that the shortest path between any two points in a plane is a straight line, we can say that the shortest path between the corresponding points on the surface is simply the image of this straight line under the isometry. Of course, the catch is that we are not using an isometry between the plane and the entire box - there is no such thing. It is the restriction of an unpacking scheme to a subset of the box that is an isometry.
|
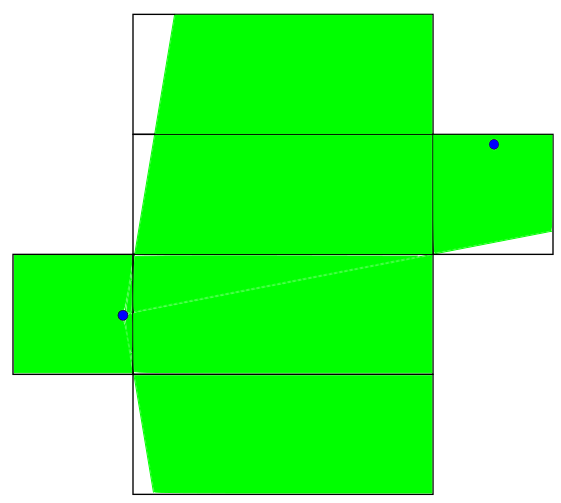
|
The same two nets are shown above and this time there is a shaded region. This represents the subset of the box to which we must restrict ourselves if we want distances to still be preserved. A path between the male ant and any green point will have the same length on the folded box as on the unfolded box. The distances found above are different because neither is contained in both shaded regions. The path of length 40.7 goes outside the right image's "safe zone" and the path of length 40 goes outside the left image's "safe zone". We've drawn two safe zones so far but there are many more.
As a bit of a digression, finding the distinct nets for a polyhedron is not necessarily easy. A 1998 paper counts the number of nets for large polyhedra and polytopes and the procedure is quite involved. There are 11 distinct nets of a cube. We can use this to find out how many distinct nets produce a rectangular prism with a square base. We can start with a cubic net like this one:

We can then choose one face not to elongate. Whether or not another face gets elongated is now completely determined by this so there are initially six ways to turn this into one of the rectangular nets we need. However, only three of them will be distinct because whenever you choose one face not to elongate, you could have just as easily chosen the face across from it and got the same result. This particular cube net produces three rectangular prism nets, but we are not done.
|
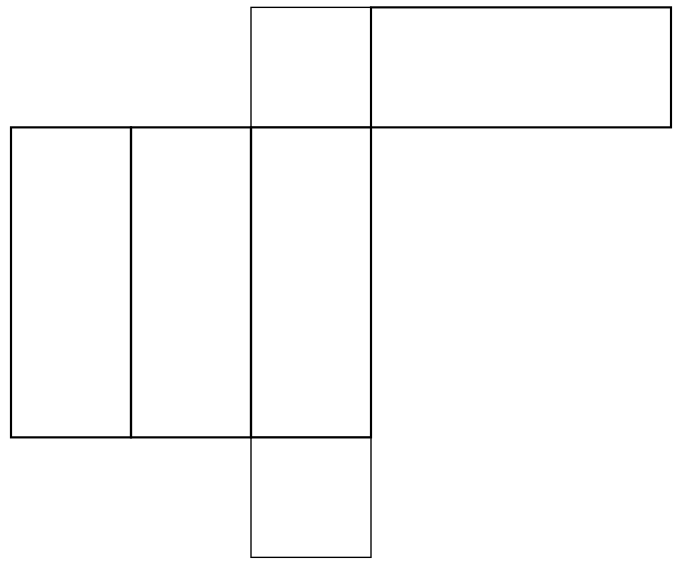
|
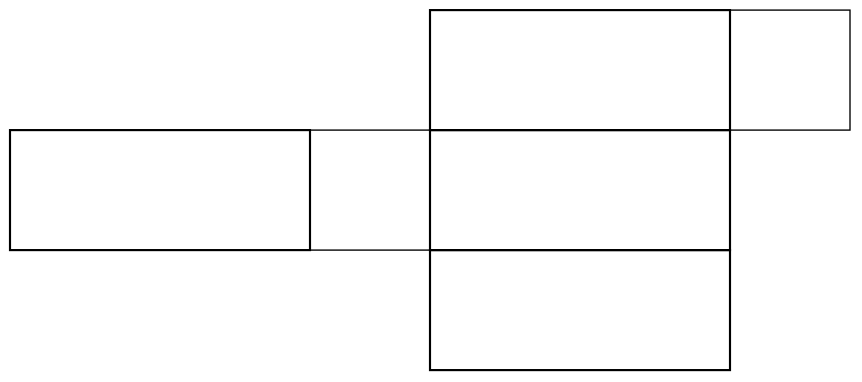
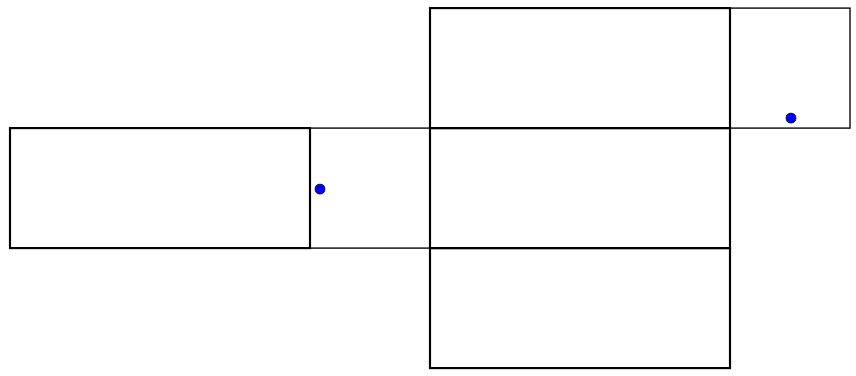
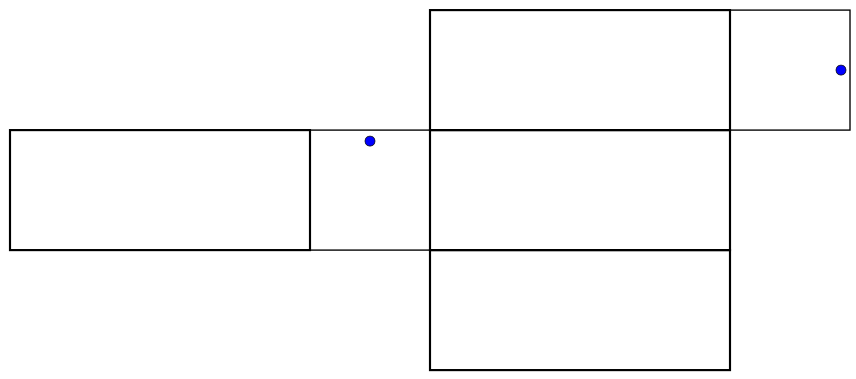
When we make a cut through the box in order to unfold it, it matters whether we are cutting below the ant, above it, or on the sides - so for each one of the above diagrams, there are really four possibilities for what its safe zone could be. The four possibilities for the bottom net are shown below.
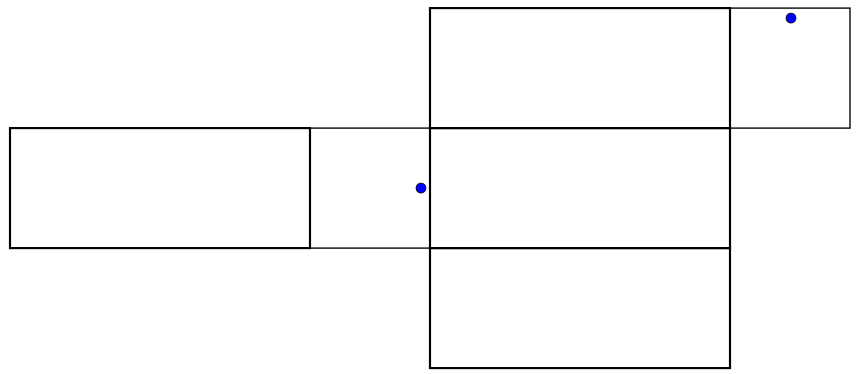
|
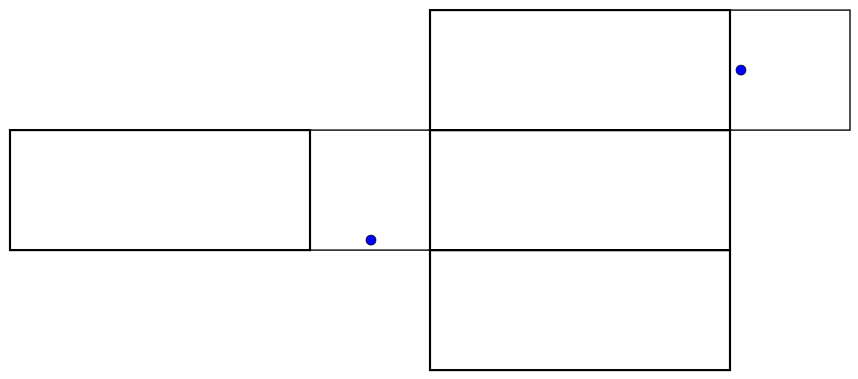
|
|
|
We start with 11 choices, each of these gives rise to 3 further choices and each of these gives rise to 4 further choices. So by this logic, the number of planar ant problems to consider is
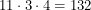 . I doubt that anyone in the class considered this many cases. Even if they did, it wouldn't matter because there are an infinite number of ways to unpack a shape! If you draw the 132 nets in the procedure that was just described, you will not get this one:
. I doubt that anyone in the class considered this many cases. Even if they did, it wouldn't matter because there are an infinite number of ways to unpack a shape! If you draw the 132 nets in the procedure that was just described, you will not get this one: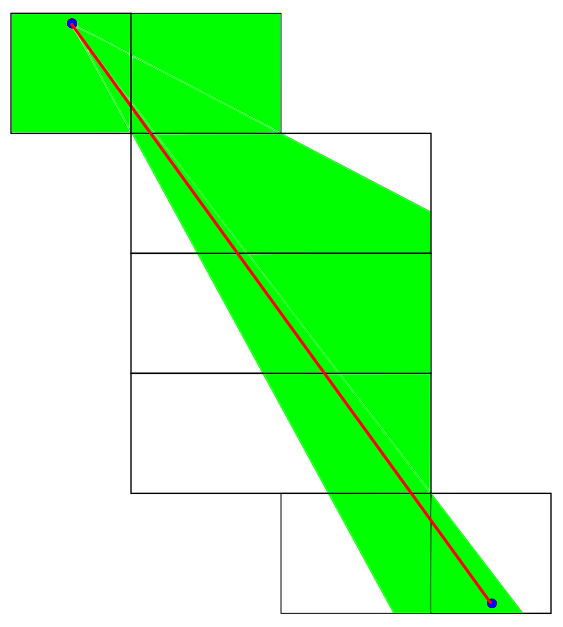
If you keep drawing nets like this until you have hundreds more, it will still be easy to think of a net that was missed. Now you might be saying that I cheated. I produced the net above by cutting through one of the faces while the 132 canonical nets only allowed cutting through the edges. But nothing is wrong with this. This is a perfectly valid mapping between the box and the plane and the red path I drew would not be within the safe zones of any of the previous 132, so we need this net. No matter how many nets you draw, you will always be able to find a path that goes outside all of their safe zones requiring you to draw one more. Maybe you're thinking that eventually these nets become so esoteric that they can't possibly yield the shortest path anymore - but that requires proof! Proving that we can get away with the net at the top of this post is the entire problem we are trying to solve!
This is what stumped us during the Math Investigations class. When students warmed up to the idea of unpacking the box in many strange ways, they asked how many times the box would have to be unpacked. We didn't have an answer, and the longer we thought about it, the more we realized that the process would never finish. This is a hard problem so we admitted that there could easily be a path with a length shorter than 40 and we didn't know how to prove it either way. Now that I've come back to the problem, I've thought up a proof that I didn't think of before and it is nice and elementary. Please tell me if you find it as convincing as I do.
Before I get into the proof, I should say that it was inspired by a problem I had to solve in one of my fourth year courses - computational commutative algebra. We were learning the theory of Gröbner bases and for an ideal in a polynomial ring, one traditionally computes the Gröbner basis by first choosing a monomial order and then applying Buchberger's algorithm. I was asked to find all possible Gröbner bases for a particular ideal. This seemed like an impossible task at first since there are an infinite number of monomial orders. However, you don't actually need to know the monomial order in its entirety. You just need to know how it ranks certain monomials and during any step in the algorithm, there are only a finite number of ways in which the monomials can be ranked. So by only choosing as much as I had to, I was able to get the Buchberger algorithm to split into a finite number of child Buchberger algorithms at each step and eventually, all the child processes finished and I got the answer (I was by no means the first person to think of doing this). This divide and conquer technique is amazingly powerful.
You don't have to know what any of this means but the conceptual situation here is similar. Running the algorithm is travelling along a path and keeping track of your distance. The infinitude of cases comes from the fact that there are infinitely many nets. For a given net, the algorithm is guaranteed to finish - we either get to the female ant in record time, or we discover that the path we are on has a length longer than 40 and we quit because we know we cannot be on the shortest path anymore. If we want to find the shortest distance between two points on adjacent faces of the box, this is surely a straight line because a subset of the cube containing only two adjacent faces can be completely mapped onto the plane using an isometry. At any given time, the only boundaries we ever cross are between adjacent faces, so instead of having to specify all unfoldings beforehand, at any given time, our unfolding only needs to be specified enough to accommodate the boundaries we have crossed so far. Without further ado, I will show you this whole process pictorially:
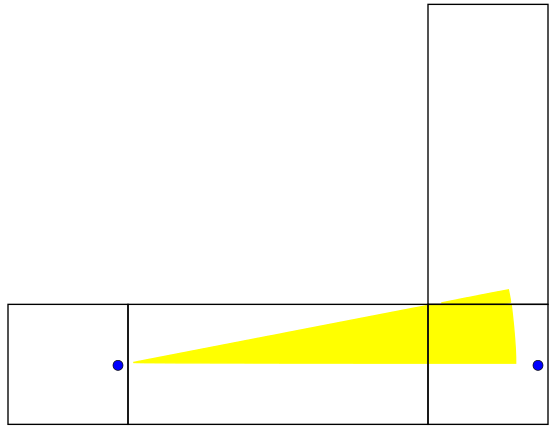
We begin our length 40 line in the horizontal direction at angle
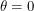 . When discussing angles here, we will let
. When discussing angles here, we will let 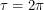 . We can rotate the line without changing the boundaries we cross until we get to
. We can rotate the line without changing the boundaries we cross until we get to 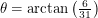 . Notice how we've only specified the important parts of the net here. The next net is valid for
. Notice how we've only specified the important parts of the net here. The next net is valid for 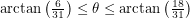 :
: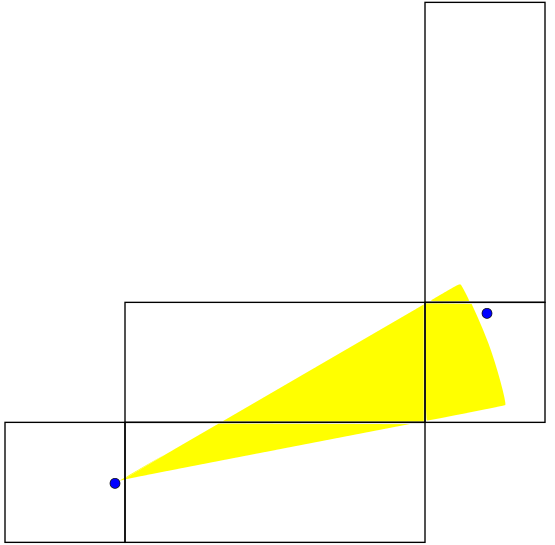
This is a familiar situation - one in which we come 0.7 units away from hitting the female ant. Close but no cigar. The next net is valid for
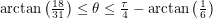 :
: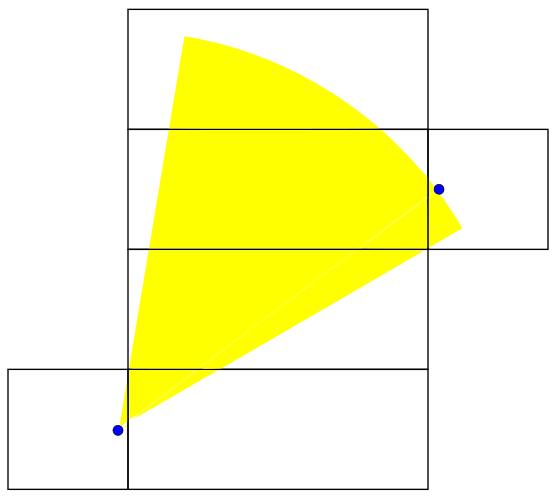
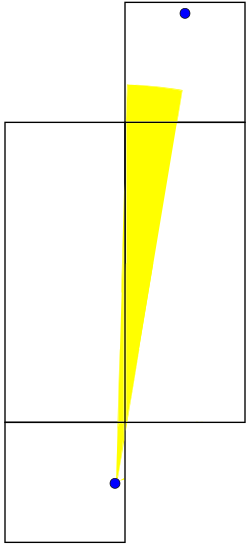
This range includes the path that allows us to hit the female ant using 40 length units. If the rest of the angles we sweep out don't allow us to do this, we will have proven that 40 is the shortest distance. The next one works for
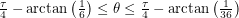 :
:
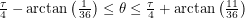
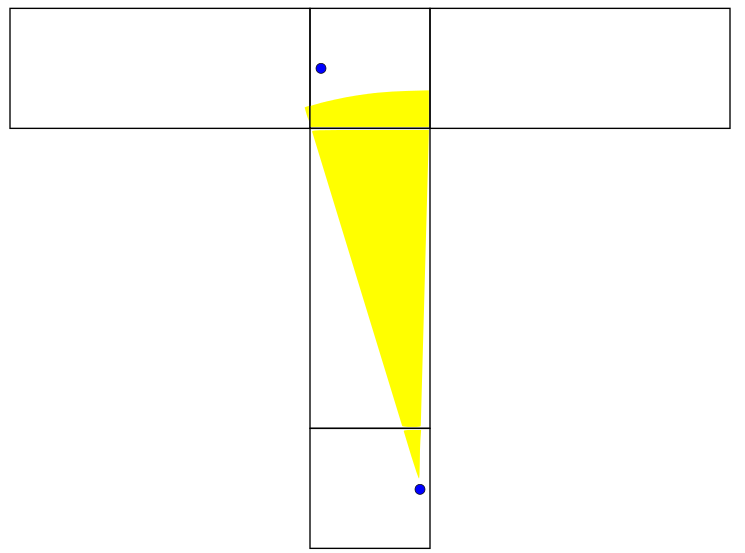
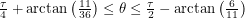
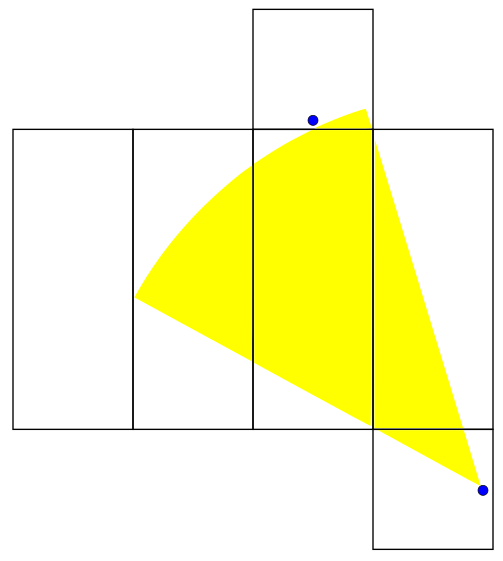
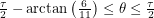
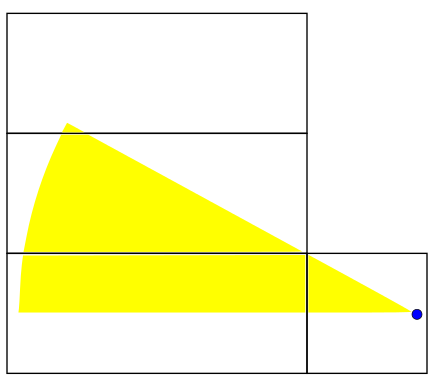
This brings us back to the axis of symmetry of the problem. We have found that no matter what our initial heading is, we will travel for at least 40 distance units before bridging the two ants. Sweeping out a path of length 40 and adjusting the net used to match the angle... it's so simple! I can't believe I didn't think of it before! Anyway, what we suggested to the first years would've used much higher level math. We talked about how the great circle is the shortest path between two points on a sphere as proven by the calculus of variations. We proposed that a similar proof could be done for a box in principle but said that it would be hard. We didn't expect any of them to know the details of how to do that calculation. We tried to give a brief survey of what variational methods are in the remaining minutes, so this is something I might talk about later.
