You are here

Home

It's Getting Hot In Here

Sun, 07/08/2011 - 22:56 — root

In a recent post, we used trigonometry to derive the length of a day on the Earth as a function of the observer's latitude and the time of year. As promised, I want to continue modelling the Earth's orbit to see what it can tell us about temperature. The simplest explanation for the seasonal variation of temperature comes from the concept of solar flux. To see what this means, think about taking a ray of sunlight shining on the Earth and decomposing it into two components - one parallel to the Earth's surface and one perpendicular.
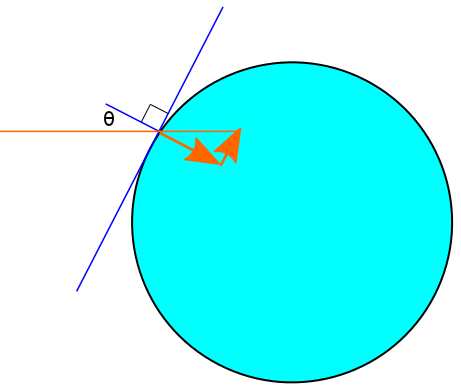
Decomposing a ray of sunlight into two components to find the flux.
Most of the sunlight going into the ground means this location will be hot, whereas most of the sunlight going along the ground means this location will be cold. The temperature due to direct sunlight is therefore proportional to the cosine of the angle between the ray and the outward normal to the Earth. To actually solve for a temperature, we would have to multiply the intensity of the light by 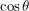$ \cos \theta $ and integrate this over a region of interest. Our main concern will be solving for 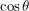$ \cos \theta $, allowing us to express the temperature at one time relative to the temperature at another time without knowing the absolute intensity.

To do this, we need a method for keeping track of the Sun's position in the sky. We can do this using the familiar angles of latitude and longitude. This standard geographic co-ordinate system projected onto the sky is called the celestial sphere. If the Sun has a latitude of 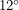$ 12^{\circ} $ and a longitude of 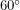$ 60^{\circ} $ on the celestial sphere, this means that the location on Earth having 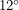$ 12^{\circ} $ latitude and 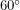$ 60^{\circ} $ longitude will see the Sun as being directly overhead. Astronomers would instead say that the Sun has a 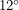$ 12^{\circ} $ declination and a $ 4 \; \textup{hour} $ right ascension but for all intents and purposes, this means the same thing.

At any point in time, there is a "sunny spot" - a latitude and longitude on the Earth where the Sun is directly overhead. We will denote this point by 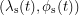$ (\lambda_{\textup{s}}(t), \phi_{\textup{s}}(t)) $. In the following diagram, we see two angles, the sunny latitude and the angle between a direct sun ray and the Earth's axis. This was a very important angle in the last post which we called 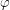$ \varphi $. 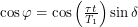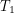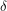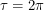The formula we had before said that $ \cos \varphi = \cos \left ( \frac{\tau t}{T_1} \right ) \sin \delta $ where $ T_1 $ is 365.24 days, $ \delta $ is the inclination of the Earth's axis and $ \tau = 2\pi $. 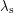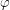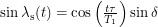Together, $ \lambda_{\textup{s}} $ and $ \varphi $ form a right angle, so the formula we are looking for is $ \sin \lambda_{\textup{s}}(t) = \cos \left ( \frac{t \tau}{T_1} \right ) \sin \delta $.
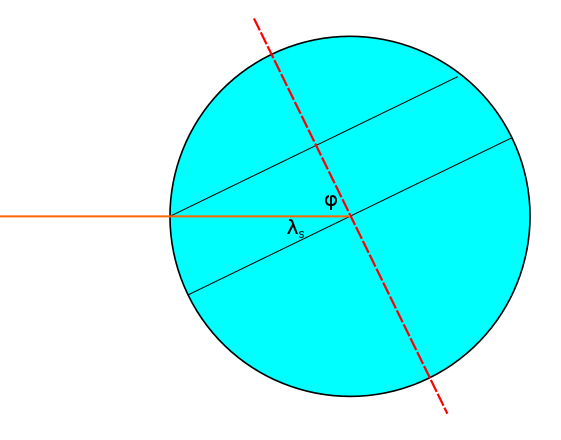
Solving for the sunniest latitude.
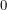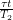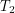Naturally, the sunny latitude must be somewhere between the Tropic of Cancer and the Tropic of Capricorn. The sunny longitude simply goes from $ 0 $ to $ \tau $ in the course of a day so a possible formula for it would be $ \frac{\tau t}{T_2} $ where $ T_2 $ is 24 hours. This formula however, is naive because after many days, the sunny longitude at the beginning of the day will be affected by the Earth's orbit. The offset this introduces is 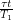$ \frac{\tau t}{T_1} $, giving us:

\[ \left ( \lambda_{\textup{s}}(t), \phi_{\textup{s}}(t) \right ) = \left ( \arcsin \left ( \cos \left ( \frac{\tau t}{T_1} \right ) \sin \delta \right ), \tau t \left ( \frac{1}{T_1} + \frac{1}{T_2} \right ) \right ) \]

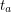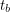When I first wrote down this function for tracking the position of the Sun with time, I first asked myself is it injective? It is actually not. In a given year, there are a few moments in time that allow the Sun's position at that time to be revisited once again in the same year. Let's demand that the latitudes be equal at times $ t_a $ and $ t_b $. This gives us:

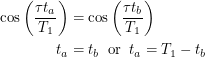\begin{align*} \cos \left ( \frac{\tau t_a}{T_1} \right ) &= \cos \left ( \frac{\tau t_b}{T_1} \right ) \\<br /> t_a &= t_b \;\; \mathrm{or} \;\; t_a = T_1 - t_b<br /> \end{align*}

Demanding the same thing for the longitudes gives us:

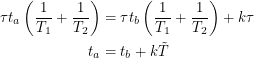\begin{align*} \tau t_a \left ( \frac{1}{T_1} + \frac{1}{T_2} \right ) &= \tau t_b \left ( \frac{1}{T_1} + \frac{1}{T_2} \right ) + k \tau \\<br /> t_a &= t_b + k \tilde{T}<br /> \end{align*}

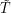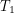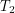where $ \tilde{T} $ is the harmonic mean of $ T_1 $ and $ T_2 $ - approximately 23.9 hours. Putting these together, we see that if the time is a half-integer multiple of 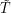$ \tilde{T} $ before the midpoint of a year, we will get another chance to see the Sun in the same place if we wait for the same half-integer multiple of 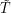$ \tilde{T} $ after the midpoint of that year. One thing I might try to do is use this information to time a visit to the Canadian War Museum in Ottawa. The window in Memorial Hall is positioned so that it will be illuminated at 11 a.m. on November 11. In order to see it light up at a different time, I could try going at 1 p.m. on February 19. Results will probably vary because how close this hour is to one of the special hours depends heavily on the leap-year cycle.

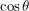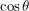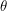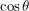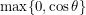Before I got distracted, the original purpose of this was to calculate $ \cos \theta $ but we should not keep saying $ \cos \theta $ because the flux is only proportional to this number when we are talking about the light side of the Earth. When the angle $ \theta $ puts us on the dark side of the Earth, the flux is zero. So the function we are really trying to find is not $ \cos \theta $ but $ \max \{ 0, \cos \theta \} $. Note that this does not mean that the temperature is zero. The flux of sunlight is only one of the factors determining temperature. The Earth's atmosphere does a good job of ensuring that places still stay relatively warm during the night. If we were on a planet with no atmosphere, nightfall really would bring about a huge drop in temperature. The next diagram shows a situation in which the Sun is just barely able to deliver a non-zero flux.
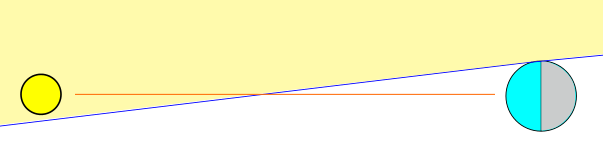
A point on the Earth where the Sun is just barely visible on the horizon.
For the location in this picture, the Sun has either just risen or is just about to set. If we assume that the Sun is very far away, the Sun will stay in the field of view until we move to the "very top" of the circle or the "very bottom". We will now use this approximation to solve for the flux at noon for an arbitrary latitude.
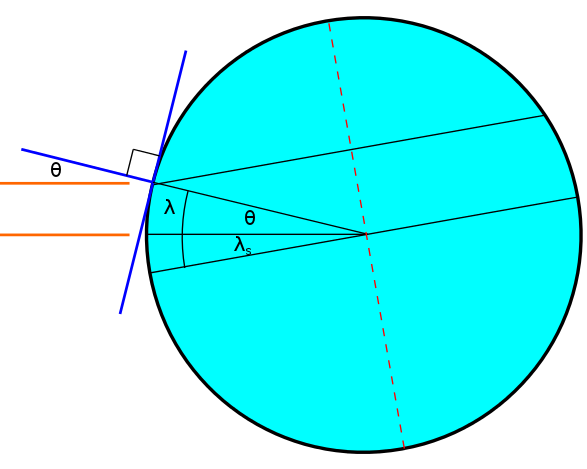
The diagram relating the flux angle to the observer's latitude and the sunny latitude.
When we solve for the flux at solar noon, we only have to worry about the latitude of the observer. The longitude will be equal to 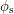$ \phi_{\textup{s}} $. The diagram above makes it clear that 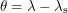$ \theta = \lambda - \lambda_{\textup{s}} $. This relies on the fact that the orange lines are parallel which is only true if we make the approximation that the Sun is infinitely far away. Making substitutions, we see that our flux is:

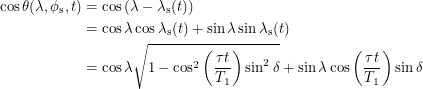\begin{align*} \cos \theta(\lambda, \phi_{\textup{s}}, t) &= \cos \left ( \lambda - \lambda_{\textup{s}}(t) \right ) \\<br /> &= \cos \lambda \cos \lambda_{\textup{s}}(t) + \sin \lambda \sin \lambda_{\textup{s}}(t) \\<br /> &= \cos \lambda \sqrt{1 - \cos^2 \left ( \frac{\tau t}{T_1} \right ) \sin^2 \delta} + \sin \lambda \cos \left ( \frac{\tau t}{T_1} \right ) \sin \delta<br /> \end{align*}

The thing we must do now is plot this function. Again, the plot confirms many intuitive things. The equator achieves the maximum temperature of one on each solstice but any other latitude between the tropics does too. In order to see days in which the warmest temperature might still be zero, we have to go above the Arctic circle or below the Antarctic circle. In other words this is equivalent to finding locations with 24 hour night.
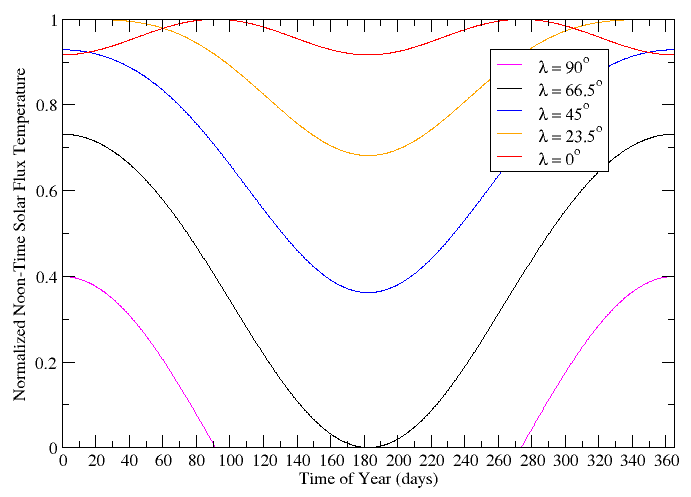
A plot showing the noon-time temperature as a function of time for various latitudes.
We solved for 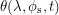$ \theta(\lambda, \phi_{\textup{s}}, t) $ but a more general quantity to calculate is 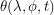$ \theta(\lambda, \phi, t) $. If you have forced yourself to visualize all of the operations up to this point, it is not too hard to see that we start off on the ray of sunlight, rotate through an angle of 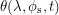$ \theta(\lambda, \phi_{\textup{s}}, t) $ in one plane and then rotate in an orthogonal plane until we get to a longitude of 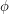$ \phi $. Recalling the sunrise post, we did something very similar. 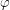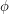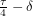We derived a relationship between the angles $ \varphi $, $ \phi $ and $ \frac{\tau}{4} - \delta $. 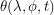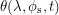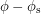The exact same relationship holds between $ \theta(\lambda, \phi, t) $, $ \theta(\lambda, \phi_{\textup{s}}, t) $ and $ \phi - \phi_{\textup{s}} $ - the cosine of the first is equal to the cosine of the second times the cosine of the third. All in all, we have:

\begin{align*} \cos \theta(\lambda, \phi, t) &= \cos \left ( \lambda - \lambda_{\textup{s}}(t) \right ) \cos \left ( \phi - \phi_{\textup{s}} \right ) \\<br /> &= \left [ \cos \lambda \sqrt{1 - \cos^2 \left ( \frac{\tau t}{T_1} \right ) \sin^2 \delta} + \sin \lambda \cos \left ( \frac{\tau t}{T_1} \right ) \sin \delta \right ] \cos \left ( \phi - \tau t \left ( \frac{1}{T_1} + \frac{1}{T_2} \right ) \right )<br /> \end{align*}

If you want this presented visually, you'll have to do it because I cannot think of a nice way to plot this beast.

Tags: 
fun calculations
space

Valid CSS and XHTML | Released under a Creative Commons License | Mobile version