The Sunrise Equation

Sun, 10/07/2011 - 21:50 — root

In my quest to watch a sunrise recently, I had to search the web to find out the time before which I needed to get up. Predicting the sunrise is something that I had pondered before. I'm sure numerical simulations are more accurate, but I began deriving a simple formula. Everyone knows the gist of why the Sun rises and sets and why this experience depends on your location on the globe. The answer is that it all depends on the tilt of the Earth's axis.

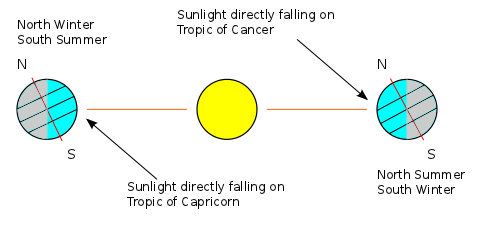
The relationship between the tropics and the solstices.

The Earth's axis of rotation makes a certain angle with the normal to the plane in which it orbits. This angle of inclination is 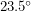$23.5^{\circ}$ . It is not hard to picture how this affects the seasons and why the tropics are offset from the equator by 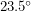$23.5^{\circ}$ as well. I found it much harder to visualize the effect that the inclination has on the length of a day and most people I've talked to simply take it on faith that the Arctic and Antarctic circles are at 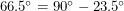$66.5^{\circ} = 90^{\circ} - 23.5^{\circ}$ latitude.

So now is our chance to overcome this hurdle. Together, you and I will figure out how to calculate the length of a day as a function of time for all latitudes. Hint: it is not a smooth function!

For convenience, let 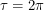$\tau = 2\pi$ . If we put the Sun at the origin of our co-ordinate system, we can track the Earth's position using polar co-ordinates 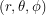$(r, \theta, \phi)$ . If we assume that Earth undergoes a circular orbit (which is almost true), we can take $r$ to be constant and not worry about it. We also know that bound orbits (circular or not) lie in a plane so we might as well use one angle to describe the orbit instead of two. 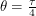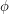What we always do in celestial mechanics is take $\theta = \frac{\tau}{4}$ and let $\phi$ vary.

We will let 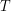$T$ be the period of Earth's revolution (1 year). Since the Earth orbits the Sun at a constant velocity, the angle through which it has revolved is given by 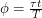$\phi = \frac{\tau t}{T}$ . Below, the Earth's axis is shown in red and the angle of inclination is labelled 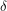$\delta$ . This diagram shows that the angle between the direct ray of sunlight (orange) and the Earth's axis depends on both 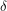$\delta$ and $\phi$ . 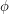One can imagine that we go "over" by 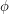$\phi$ and then "up" by 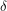$\delta$ and we need to know what the overall angle is.

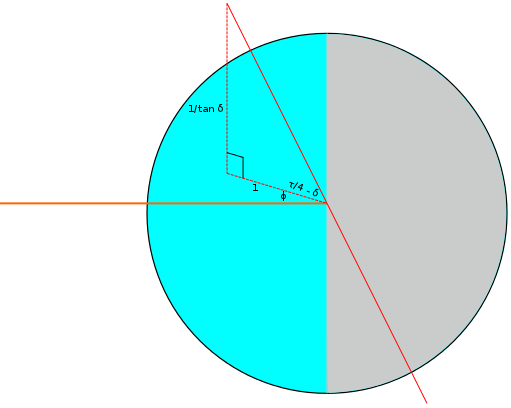
Calculating the angle between a direct ray of sunlight and the Earth's axis.

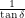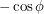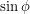If we let the x-axis be horizontal, the z-axis be vertical and the y-axis point out of the page, the third component of a vector pointing along Earth's axis can be $\frac{1}{\tan \delta}$ . The first two components must then be $-\cos \phi$ and $\sin \phi$ so that the foot of the perpendicular will have unit length as we have drawn it. We must therefore find the angle between 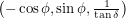$\left ( -\cos \phi, \sin \phi, \frac{1}{\tan \delta} \right )$ and a vector pointing from the Earth to the Sun, say 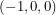$(-1, 0, 0)$ . Solving for the absolute angle, 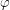$\varphi$ , is not too difficult.

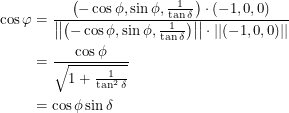$\begin{align*} \cos \varphi &= \frac{\left ( -\cos \phi, \sin \phi, \frac{1}{\tan \delta} \right ) \cdot (-1, 0, 0)}{\left | \left | \left ( -\cos \phi, \sin \phi, \frac{1}{\tan \delta} \right ) \right | \right | \cdot \left | \left | (-1, 0, 0) \right | \right |} \\<br /> &= \frac{\cos \phi}{\sqrt{1 + \frac{1}{\tan^2 \delta}}} \\<br /> &= \cos \phi \sin \delta \end{align*}$

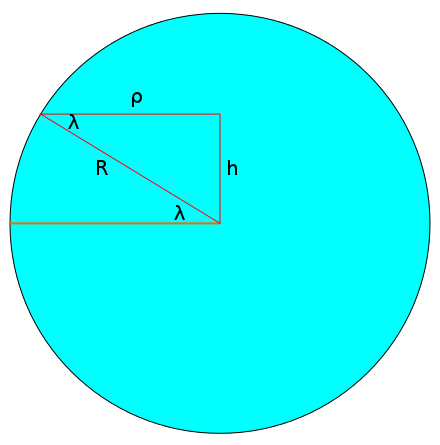
Now we need to figure out how the length of a day depends on 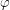$\varphi$ . In the next diagram, we have chosen an arbitrary latitude above the equator and drawn it as a circle around the Earth. This circle has a radius of 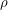$\rho$ and from the centre of this circle, you get to the centre of the Earth by travelling a distance of 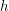$h$ down the red axis.

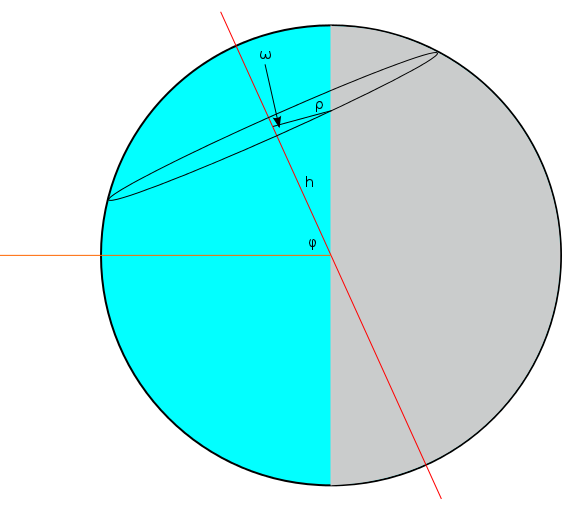
A line of latitude where the day is longer than 12 hours.

Now clearly, the latitude we have drawn has a day that is longer than 12 hours. More than half of the circumference of the circle lies in the blue "lit up" part of the Earth. We quantify the amount by which the day is longer using an "overflow angle" $\omega$ . There is an $\omega$ on both sides, so the length of a day is equal to 24 hours times 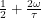$\frac{1}{2} + \frac{2 \omega}{\tau}$ . 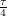Notice that if we had chosen a line of latitude that was a bit farther North but still below the North Pole, it would lie entirely in the blue section, $\omega$ would be equal to $\frac{\tau}{4}$ and the day would be 24 hours long. We will see that this extreme comes out nicely in the final equation.

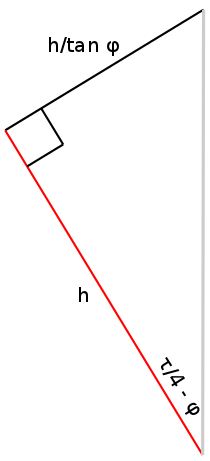
A triangle where we do some trigonometry.

To find the length of the bright piece of the circle that is left after it has already gone halfway around, we can consider parallel lines that pass through the endpoints of this arc. The end of this arc can be found if we start at the point on the circle that crosses the blue/gray boundary and draw the perpendicular from that point to the vertical untilted line. The beginning of this arc can be found if we instead draw a line (of length 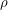$\rho$ ) from this same point to the centre of the circle and rotate it back through an angle of $\omega$ . The rotated line will then intersect the beginning of the arc. In the triangle above, we can draw a line sticking out of the page at the top-left corner that will intersect the beginning and we can draw a parallel line, also sticking out of the page, at the top-right corner that will intersect the end. 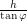It is useful to solve for the length of the line segment joining them, which is $\frac{h}{\tan \varphi}$ . This line segment is straight, so it cannot be the curved arc we are looking for. Rather, it is tangent to the circle in the following way:

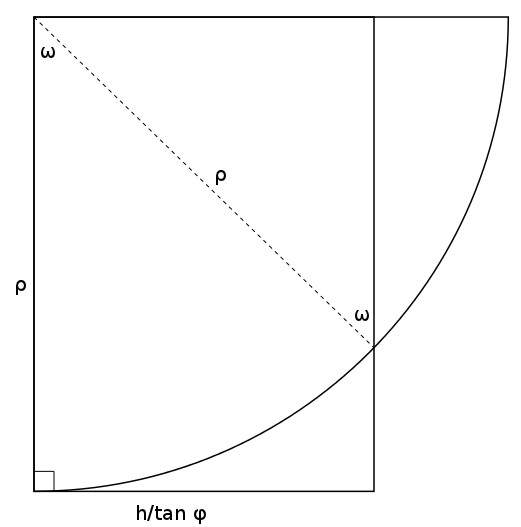
Another triangle where we do some trigonometry.

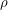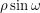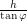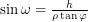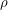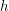Consider the triangle in the upper-right corner having a hypotenuse of $\rho$ . The leg of this triangle on the top has a length of $\rho \sin \omega$ since one of its angles is $\omega$ . But this length is also equal to $\frac{h}{\tan \varphi}$ since the overall shape is a rectangle. We now have $\sin \omega = \frac{h}{\rho \tan \varphi}$ . It remains to be seen how $\rho$ and $h$ depend on the latitude. These are expressions you might have guessed. Below we denote the latitude by 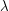$\lambda$ and the radius of the Earth by 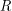$R$ . 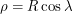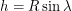It follows immediately that $\rho = R \cos \lambda$ and $h = R \sin \lambda$ .

Radii and heights in terms of latitudes.

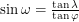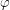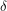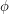Substituting this into the expression above, we get $\sin \omega = \frac{\tan \lambda}{\tan \varphi}$ . A constraint of the problem is now apparent. The sine of a physical angle should be between -1 and 1 right? Going back to the diagram where we calculated $\varphi$ in terms of $\delta$ and $\phi$ , it is clear that 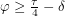$\varphi \geq \frac{\tau}{4} - \delta$ which means 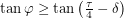$\tan \varphi \geq \tan \left ( \frac{\tau}{4} - \delta \right )$ . So if 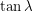$\tan \lambda$ were less than 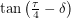$\tan \left ( \frac{\tau}{4} - \delta \right )$ , it couldn't possibly also be greater than 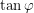$\tan \varphi$ . This means that 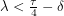$\lambda < \frac{\tau}{4} - \delta$ guarantees us an angle $\omega$ that makes sense. 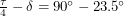Conversely, latitudes on the other side are greater than $\frac{\tau}{4} - \delta = 90^{\circ} - 23.5^{\circ}$ which means they are above the Arctic circle or below the Antarctic circle. It is these regions that sometimes have 24 hours of light or 24 hours of darkness. The existence of days without sunlight ensures that the tree line also resides at a 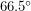$66.5^{\circ}$ latitude because most plants above this line are not able to survive throughout the year.

We have not yet put all of our useful information together. We know that 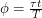$\phi = \frac{\tau t}{T}$ , we know that 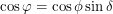$\cos \varphi = \cos \phi \sin \delta$ , we know that as a fraction of 24 hours, a day is 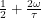$\frac{1}{2} + \frac{2 \omega}{\tau}$ and we know that 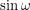$\sin \omega$ is equal to 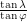$\frac{\tan \lambda}{\tan \varphi}$ , rounded down if it is above 1 and rounded up if it is below -1. The last step required to find the length $L$ is:

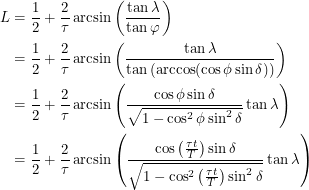$\begin{align*} L &= \frac{1}{2} + \frac{2}{\tau} \arcsin \left ( \frac{\tan \lambda}{\tan \varphi} \right ) \\ &= \frac{1}{2} + \frac{2}{\tau} \arcsin \left ( \frac{\tan \lambda}{\tan \left ( \arccos (\cos \phi \sin \delta ) \right )} \right ) \\<br /> &= \frac{1}{2} + \frac{2}{\tau} \arcsin \left ( \frac{\cos \phi \sin \delta}{\sqrt{1 - \cos^2 \phi \sin^2 \delta}} \tan \lambda \right ) \\<br /> &= \frac{1}{2} + \frac{2}{\tau} \arcsin \left ( \frac{\cos \left ( \frac{\tau t}{T} \right ) \sin \delta}{\sqrt{1 - \cos^2 \left ( \frac{\tau t}{T} \right ) \sin^2 \delta}} \tan \lambda \right ) \end{align*}$

It is fun to plot this function and confirm our intuition about sunrises and sunsets. To go from day length to actual sunrise and sunset times, all we have to do is remember that our system of keeping time is setup so that 12:00 noon occurs in the middle of a day. This is valid when you are in the centre of your timezone. Let's say that you are two thirds of the way between the west edge and east edge of your timezone (the real edge, not the bendy edge). This means that the solar noon for your location actually occurs 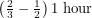$\left ( \frac{2}{3} - \frac{1}{2} \right ) 1 \; \textup{hour}$ earlier than noon - i.e. 11:50am. If you evaluate the function we just derived and find that 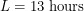$L = 13 \; \textup{hours}$ , sunrise can be expected 6.5 hours earlier than noon: 5:20 am. This of course becomes 6:20 am if you want it in daylight time.

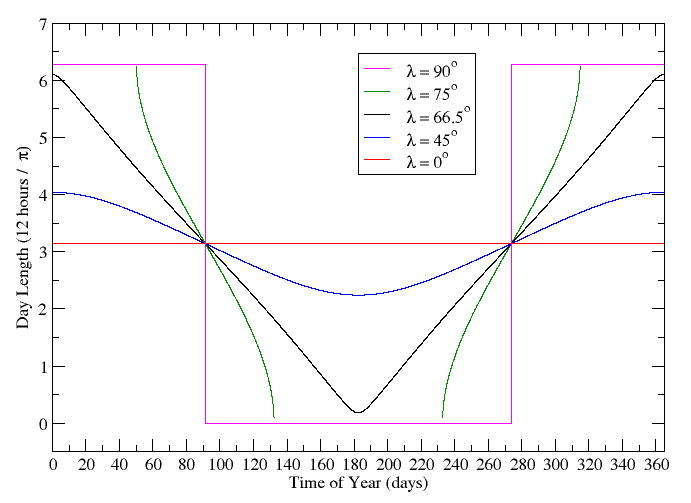
Plotting the function we have derived for representative latitudes.

This approach does a good job of predicting when locations around the globe receive light, but can it tell us anything about temperature? Temperature is harder because it depends heavily on terrestrial factors and only a rough approximation can be calculated geometrically. I wouldn't want to change notation on you in the middle of a post so I guess you'll have to stay tuned and read the next one!

Tags:

fun calculations

space

Main menu

Navigation

You are here