You are here

Home

Simple Language Benchmark

Tue, 27/09/2011 - 18:46 — root

As some of you may know, the programming languages I use the most are C and Python. One reason for this is popularity - I want to learn something that will help me edit the programs I use. I also think it's good to know at least one compiled language and one interpreted language. Interpreted languages or "scripting languages" are more convenient in most respects but they take longer to run. I already knew Python would be slower than C but I wanted to see how much slower.
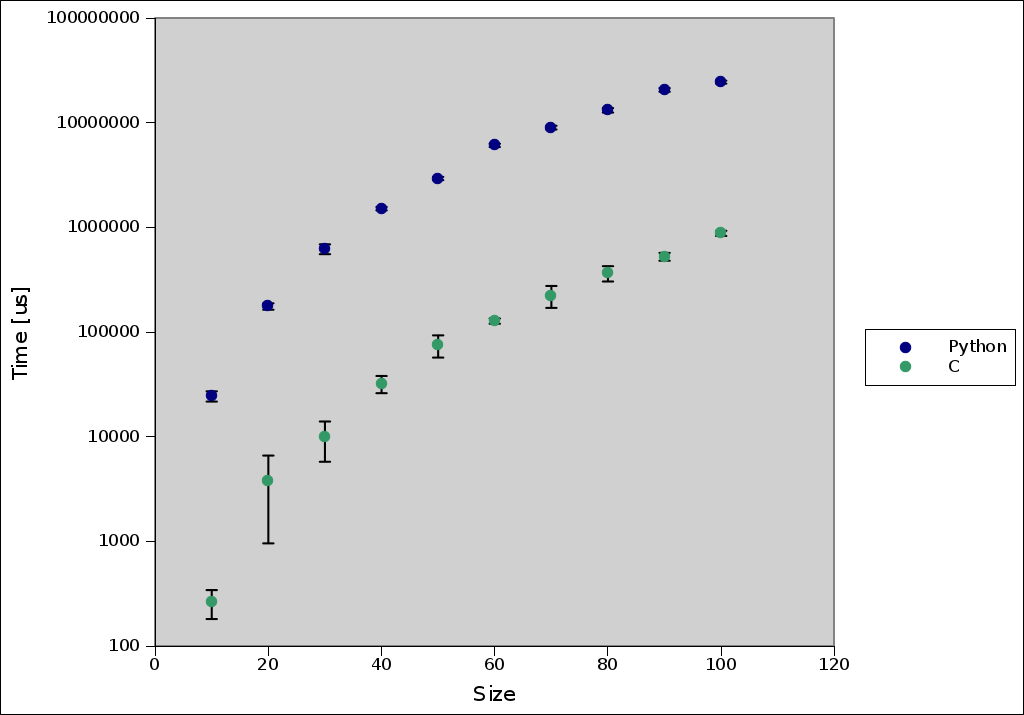
Plot showing how long C and Python codes took to diagonalize various matrices.
To make the above plot, I used C and Python codes to diagonalize an n by n matrix and kept track of their execution times. Once you get past the small matrices, the trend that begins to emerge is that Python is ~30 times slower than C.

Of course, there is more to say. I need to convince you that this was a fair test! Both programs were run on my ancient Pentium III laptop. My C program, matrixtimer.c was compiled with GCC and the optimization flags -march=pentium3 -Os -fomit-frame-pointer -pipe. My Python program, matrixtimer.py was byte compiled by opening a Python 2.7 shell and typing import matrixtimer. When testing each piece of code, I supplied the matrix size n, as an argument, and ran the diagonalization routine five times. Each data point in the plot shows the mean from those five trials with an error bar equal to the standard deviation.

Now there is the question of what eigenvalue algorithm I used. If you're big on numerics, look at the code here and see if you can guess! Otherwise I'll tell you in the next paragraph.

matrixtimer.c

  1. #include <stdio.h>
  2. #include <stdlib.h>
  3. #include <math.h>
  4. #include <time.h>
  5. #include <sys/time.h>
  6. #define TOLERANCE 0.1
  7.  
  8. void find_max(double **matrix, int size, int *p, int *q) {
  9. 	double max;
  10. 	int i, j;
  11.  
  12. 	max = 0.0;
  13.  
  14. 	for (j = 0; j < size; j++) {
  15. 		for (i = 0; i < j; i++) {
  16. 			if (matrix[i][j] > max) {
  17. 				max = matrix[i][j];
  18. 				*p = i;
  19. 				*q = j;
  20. 			}
  21. 		}
  22. 	}
  23. }
  24.  
  25. double norm(double **matrix, int size) {
  26. 	double sum_of_squares;
  27. 	int i;
  28.  
  29. 	sum_of_squares = 0.0;
  30.  
  31. 	for (i = 0; i < size; i++) {
  32. 		sum_of_squares += matrix[i][i] * matrix[i][i];
  33. 	}
  34.  
  35. 	return sqrt(sum_of_squares / ((double) size));
  36. }
  37.  
  38. void get_difference(double **a, double **b, double **difference, int size) {
  39. 	int i, j;
  40.  
  41. 	for (i = 0; i < size; i++) {
  42. 		for (j = 0; j < size; j++) {
  43. 			difference[i][j] = fabs(a[i][j] - b[i][j]);
  44. 		}
  45. 	}
  46. }
  47.  
  48. void transfer_diagonal_elements(double **dest, double **src, int size) {
  49. 	int i;
  50.  
  51. 	for (i = 0; i < size; i++) {
  52. 		dest[i][i] = src[i][i];
  53. 	}
  54. }
  55.  
  56. void diagonalize(double **matrix, double **eigenvector_matrix, int size) {
  57. 	double **diagonal_matrix = malloc(size * sizeof(double *));
  58. 	double **difference_matrix = malloc(size * sizeof(double *));
  59.  
  60. 	double sine, cosine, temp1, temp2;
  61. 	int i, j, p, q, state;
  62.  
  63. 	for (i = 0; i < size; i++) {
  64. 		diagonal_matrix[i] = calloc(size, sizeof(double));
  65. 		difference_matrix[i] = calloc(size, sizeof(double));
  66. 	}
  67.  
  68. 	transfer_diagonal_elements(diagonal_matrix, matrix, size);
  69. 	get_difference(matrix, diagonal_matrix, difference_matrix, size);
  70. 	find_max(difference_matrix, size, &p, &q);
  71. 	state = 1;
  72.  
  73. 	while (state) {
  74. 		sine = matrix[p][q] / hypot(matrix[p][q], matrix[q][q] - matrix[p][p]);
  75. 		cosine = (matrix[q][q] - matrix[p][p]) / hypot(matrix[p][q], matrix[q][q] - matrix[p][p]);
  76.  
  77. 		if (fabs(cosine) < 1e-5) {
  78. 			cosine = 1.0 / sqrt(2.0);
  79. 			sine = 1.0 / sqrt(2.0);
  80. 		}
  81.  
  82. 		for (j = 0; j < size; j++) {
  83. 			temp1 = cosine * matrix[p][j] - sine * matrix[q][j];
  84. 			temp2 = sine * matrix[p][j] + cosine * matrix[q][j];
  85. 			matrix[p][j] = temp1;
  86. 			matrix[q][j] = temp2;
  87. 		}
  88.  
  89. 		for (i = 0; i < size; i++) {
  90. 			temp1 = cosine * matrix[i][p] - sine * matrix[i][q];
  91. 			temp2 = sine * matrix[i][p] + cosine * matrix[i][q];
  92. 			matrix[i][p] = temp1;
  93. 			matrix[i][q] = temp2;
  94. 		}
  95.  
  96. 		for (i = 0; i < size; i++) {
  97. 			temp1 = cosine * eigenvector_matrix[i][p] - sine * eigenvector_matrix[i][q];
  98. 			temp2 = sine * eigenvector_matrix[i][p] + cosine * eigenvector_matrix[i][q];
  99. 			eigenvector_matrix[i][p] = temp1;
  100. 			eigenvector_matrix[i][q] = temp2;
  101. 		}
  102.  
  103. 		transfer_diagonal_elements(diagonal_matrix, matrix, size);
  104. 		get_difference(matrix, diagonal_matrix, difference_matrix, size);
  105. 		find_max(difference_matrix, size, &p, &q);
  106.  
  107. 		if (fabs(matrix[p][q]) < TOLERANCE * norm(diagonal_matrix, size)) {
  108. 			state = 0;
  109. 		}
  110. 	}
  111. }
  112.  
  113. int main(int argc, char **argv) {
  114. 	int i, j, size;
  115. 	time_t t0;
  116.  
  117. 	size = (int) strtod(argv[1], NULL);
  118.  
  119. 	double **matrix = malloc(size * sizeof(double *));
  120. 	double **identity_matrix = malloc(size * sizeof(double *));
  121.  
  122. 	for (i = 0; i < size; i++) {
  123. 		matrix[i] = calloc(size, sizeof(double));
  124. 		identity_matrix[i] = calloc(size, sizeof(double));
  125. 	}
  126.  
  127. 	t0 = time(NULL);
  128. 	srand(t0);
  129.  
  130. 	for (i = 0; i < size; i++) {
  131. 		identity_matrix[i][i] = 1.0;
  132. 		for (j = 0; j <= i; j++) {
  133. 			matrix[i][j] = 9.0 * rand() / RAND_MAX;
  134. 			matrix[j][i] = matrix[i][j];
  135. 		}
  136. 	}
  137.  
  138. 	struct timeval tv1;
  139. 	struct timeval tv2;
  140. 	int t1, t2;
  141.  
  142. 	gettimeofday(&tv1, NULL);
  143. 	t1 = tv1.tv_usec + 1000000 * tv1.tv_sec;
  144. 	diagonalize(matrix, identity_matrix, size);
  145. 	gettimeofday(&tv2, NULL);
  146. 	t2 = tv2.tv_usec + 1000000 * tv2.tv_sec;
  147.  
  148. 	printf("%d\n", t2 - t1);
  149. }

matrixtimer.py

  1. #!/usr/bin/python2
  2. import sys
  3. import math
  4. import random
  5. import timeit
  6.  
  7. def find_max(matrix):
  8. 	max = 0
  9. 	for j in range(0, len(matrix)):
  10. 		for i in range(0, j):
  11. 			if matrix[i][j] > max:
  12. 				max = matrix[i][j]
  13. 				p = i
  14. 				q = j
  15. 	return (p, q)
  16.  
  17. def norm(matrix):
  18. 	sum = 0
  19. 	for i in range(0, len(matrix)):
  20. 		sum += matrix[i][i] ** 2
  21. 	return math.sqrt(float(sum) / float(len(matrix)))
  22.  
  23. def diagonalize(matrix, eigenvector_matrix):
  24. 	tol = 0.1
  25.  
  26. 	diagonal_matrix = []
  27. 	difference_matrix = []
  28. 	for i in range(0, len(matrix)):
  29. 		current_diagonal_row = []
  30. 		current_difference_row = []
  31. 		for j in range(0, len(matrix)):
  32. 			if i == j:
  33. 				current_diagonal_row.append(matrix[i][j])
  34. 				current_difference_row.append(0)
  35. 			else:
  36. 				current_diagonal_row.append(0)
  37. 				current_difference_row.append(matrix[i][j])
  38. 		diagonal_matrix.append(current_diagonal_row)
  39. 		difference_matrix.append(current_difference_row)
  40. 	p, q = find_max(difference_matrix)
  41. 	state = True
  42.  
  43. 	while state:
  44. 		sine = matrix[p][q] / math.hypot(matrix[p][q], matrix[q][q] - matrix[p][p])
  45. 		cosine = (matrix[q][q] - matrix[p][p]) / math.hypot(matrix[p][q], matrix[q][q] - matrix[p][p])
  46.  
  47. 		if abs(cosine) < 1e-5:
  48. 			sine = 1.0 / math.sqrt(2.0)
  49. 			cosine = 1.0 / math.sqrt(2.0)
  50.  
  51. 		for j in range(0, len(matrix)):
  52. 			temp1 = cosine * matrix[p][j] - sine * matrix[q][j]
  53. 			temp2 = sine * matrix[p][j] + cosine * matrix[q][j]
  54. 			matrix[p][j] = temp1
  55. 			matrix[q][j] = temp2
  56.  
  57. 		for i in range(0, len(matrix)):
  58. 			temp1 = cosine * matrix[i][p] - sine * matrix[i][q]
  59. 			temp2 = sine * matrix[i][p] + cosine * matrix[i][q]
  60. 			matrix[i][p] = temp1
  61. 			matrix[i][q] = temp2
  62.  
  63. 		for i in range(0, len(matrix)):
  64. 			temp1 = cosine * eigenvector_matrix[i][p] - sine * eigenvector_matrix[i][q]
  65. 			temp2 = sine * eigenvector_matrix[i][p] + cosine * eigenvector_matrix[i][q]
  66. 			eigenvector_matrix[i][p] = temp1
  67. 			eigenvector_matrix[i][q] = temp2
  68.  
  69. 		for i in range(0, len(matrix)):
  70. 			diagonal_matrix[i][i] = matrix[i][i]
  71.  
  72. 		for i in range(0, len(matrix)):
  73. 			for j in range(0, len(matrix)):
  74. 				difference_matrix[i][j] = abs(matrix[i][j] - diagonal_matrix[i][j])
  75.  
  76. 		p, q = find_max(difference_matrix)
  77.  
  78. 		if abs(matrix[p][q]) < tol * norm(diagonal_matrix):
  79. 			state = False
  80.  
  81. matrix = []
  82. identity_matrix = []
  83. size = int(sys.argv[1])
  84. for i in range(0, size):
  85. 	current_row = []
  86. 	current_identity_row = []
  87. 	for j in range(0, size):
  88. 		current_row.append(random.randrange(0, 9))
  89. 		if i == j:
  90. 			current_identity_row.append(1)
  91. 		else:
  92. 			current_identity_row.append(0)
  93. 	matrix.append(current_row)
  94. 	identity_matrix.append(current_identity_row)
  95.  
  96. for i in range(0, size):
  97. 	for j in range(i, size):
  98. 		matrix[i][j] = matrix[j][i]
  99.  
  100. function_string = "diagonalize(" + str(matrix) + ", " + str(identity_matrix) + ")"
  101. t = timeit.Timer(function_string, 'from __main__ import diagonalize')
  102. time = 1000000 * t.timeit(number = 1)
  103. print time

Both files generate a matrix that is symmetric but otherwise random. Then they implement Jacobi's eigenvalue algorithm from 1846 which has a special place in my heart. The symmetric eigenvalue problem came up (as it often does) in my project for a computational physics class in my third year of undergrad. The class was very introductory so no one's project was actually going to rival modern algorithms. Rather than link to an external library to diagonalize the matrix I needed, I put in that last little bit of effort to make the program self contained. Since it involves many basic numerical tasks, I thought it would be a good benchmark.

Jacobi's algorithm is indeed slower than the symmetric eigenvalue algorithms used in standard software packages like LAPACK. My undergraduate thesis supervisor even said that the LAPACK ones were far from optimal... probably because he knows Kazushige Goto (what a great name for a programmer). Nevertheless, people are still interested in the algorithm because it can easily be split into several parallel jobs. A quick look through the C and Python examples should reveal several operations that can be done concurrently.

Tags: 
example code
tuning performance

Valid CSS and XHTML | Released under a Creative Commons License | Mobile version